Introduction
Semiconductor nanocrystals also known as quantum dots (QDs). These nanocrystals exhibit size quantization effects as an effect of their small size, resulting in a size dependence of their optical and electronic properties with respect to the bulk crystal. With decreasing particle size towards the bulk exciton Bohr radius, splitting of the energy bands will occur at the edges of the band structure. The splitting of the energy bands results in sharper energy transitions than for the bulk crystal comparable with atomic like transitions, with drastic changes in optical and electronic properties of the material.
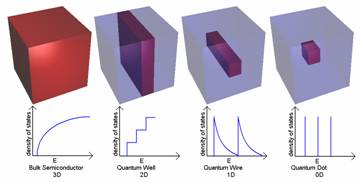
Figure 1. The effect of size on the band structure of a semiconductor crystal for four different size-ranges. The band structure of the bulk semiconductor crystal (R>>ab) with a continuous energy bands; a completely filled valance band (VB) and empty conduction band (CB), a quatum well, a quantum wire and quantum dot (R< The decrease in particle size will result in an increase in bandgap, which is reflected in a blue shift for both photo emission and absorbance. 
Figure 2. Photoluminescence of Cadmium Selenide (CdSe) QDs in solution with decreasing (big red >4nm; small blue <2 nm) particle size. The sharp and size tunable optical properties make these semiconductor types QDs, e.g. CdSe, CdTe, CdS, ZnS etc. interesting as luminescent chromophores in various applications. QDs have shown to be exciting fluorescent labels in biological research projects, where a demand was on stable highly luminescent bio-compatible labels. The very narrow and efficient optical properties of QDs make them also interesting candidates for the use in light emitting diodes (LEDs). This project is mainly focused on the synthesis different quantum dots for their application in quantum dot LEDs quantum Size Effects in Semi Conductor Nano Crystals When the radius of a QD approaches the size of the exciton Bohr radius, the motion of the electrons and holes becomes confined in the QD. This results in an increase of the band gap when the particle size is decreasing. As a consequence of spatial confinement of the charge carriers, the kinetic energy becomes quantified. Due to these so called quantum size effects absorption and emission spectra will shift to higher energies with decreasing particle size. The spatial confinement of electron and hole wavefunctions can be described by the particle in a box model. 
Where a is the radius of the semiconductor particle, and Eg represents the band gap of the bulk semiconductor. The second therm represents the particle in a box localization energy. The third term represents the Coulomb energy with 1/a dependence, the energy of a bound electron hole pair (exciton) is smaller than for a non bonded electron and hole and decreases therefore the bandgap slightly. This formula gives a good approximation for the weak confinement regime but it gives an over estimation in the strong confinement regime (very small particles). |

